バーガースベクトル

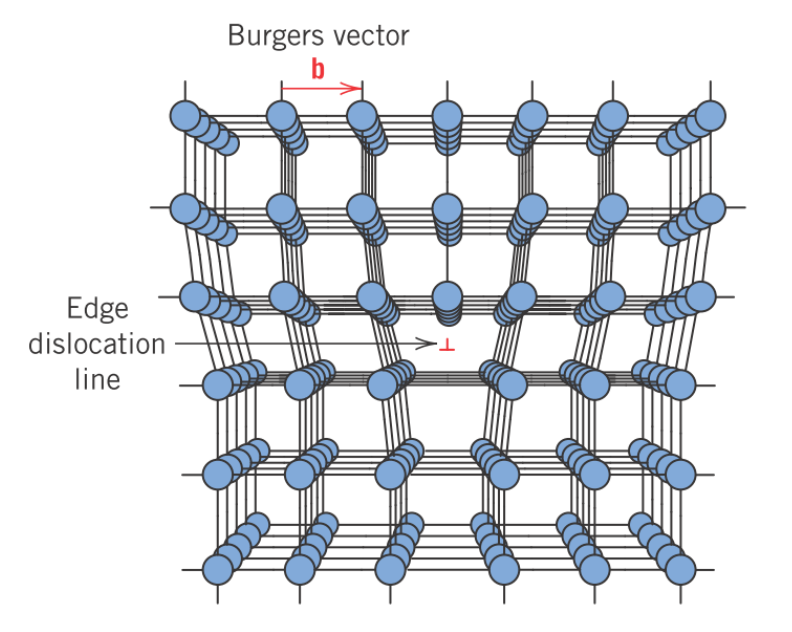
材料工学において、バーガース・ベクトル（英語: Burgers vector）とは結晶格子内の転位に起因する格子ひずみの大きさおよび方向を表すベクトル。しばしば b と書かれる。その名はオランダの物理学者ヤン・バーガースにちなむ。

ベクトルの大きさおよび方向は、転位なしの状態（完全結晶）を最初に考えると理解しやすい。この完全結晶の構造で、長さと幅が単位格子の辺の長さ(aとする)の整数倍の矩形を描いてみる。そのあと矩形の内側に転位を導入し、結晶を変形させることを考える。描いた転位点を囲む矩形はこの変形によって一部が切断されることになるが、この切断された線分を繋ぐベクトルがバーガースベクトルである。

ベクトルの方向は転位面に依存し、転位面は通常、最密格子の結晶面の1つである。大きさは通常次式で表される（BCC、FCC格子のみ）

${\displaystyle \|\mathbf {b} \|={\frac {a}{2}}{\sqrt {h^{2} k^{2} l^{2}}}}$

aは結晶の単位格子の辺長、||b||はバーガースベクトルの大きさ、h, k, l はバーガースベクトルの成分である。b = ${\displaystyle (a/2)\langle hkl\rangle }$ , 係数a/2はBBCとFCC格子において最短の格子ベクトルが${\displaystyle (a/2)\langle hkl\rangle }$と表現されるからである。比較的単純な立方格子の場合、b = ${\displaystyle a\langle hkl\rangle }$であるため、大きさは次のように表される。

${\displaystyle \|\mathbf {b} \|=a{\sqrt {h^{2} k^{2} l^{2}}}}$

大部分の金属材料においては、単一転位は最密格子の結晶面一つ分のずれであるため、転位に対するバーガースベクトルの大きさは、材料の原子間間隔と等しい大きさである。

刃状転位において、バーガースベクトルと転位線は互いに垂直である。らせん転位においてはそれらは平行である。

バーガースベクトルは、溶質硬化、析出硬化、加工硬化に影響を与えることにより材料の降伏強度を決定するのに重要である。また、転位線の方向を決定するのに重要な役割を果たす。

関連項目

• フランクリード源

脚注

外部リンク